Algorithm
面对算法问题思路
- 你会如何对一组数据进行排序?
第一想法:快速排序算法 O(nlogn)
- 深入思考:这组数据有什么样的特征?
- 有没有可能包含有大量重复的元素?
- 如果有这种可能的话,三路快排是更好的选择。
- 是否大部分数据距离它正确的位置很近?是否近乎有序?(如:时间记录,发生早但记录晚,导致顺序问题)
- 如果是这样的话,插入排序是更好的选择。
- 是否数据的取值范围非常有限?(如:学生成绩排序,分数的取值0~100左右)
- 如果是这样的话,计数排序是更好的选择。
- 额外要求:是都需要稳定排序?
- 如果是的话,归并排序是更好的选择。
- 数据的存储状况是怎么样的:是否是使用链表存储的?
- 如果是的话,归并排序是更好的选择。
- 数据的存储状况是怎么样的:数据的大小是否可以装载在内存里?
- 数据量很大,或者内存很小,不足以装载在内存里,需要使用外排序算法。
- 有没有可能包含有大量重复的元素?
优化算法思路:
- 空间和时间的交换(哈希表)
- 预处理信息(排序)
- 在瓶颈出寻找答案:O(nlogn)+O(n^2); O(n^3)
时间复杂度
n 表示数据规模
O(f(n))表示运行算法所需要执行的指令数,和f(n)成正比
举例:(a、b、c、d 皆是常数)
二分查找法 O(logn) 所需执行指令数:a*logn
寻找数组中的最大/最小值 O(n) 所需执行指令数:b*n
归并排序算法 O(nlogn) 所需执行数:c*nlogn
选择排序法 O(n^2) 所需指令数:d*n^2
算法A: O(n) 所需执行指令数:10000*n
算法B: O(n^2) 所需执行指令数:10*n^2
| n | A指令数 10000n | B指令数 10n^2 | 倍数 |
|---|---|---|---|
| 10 | 10^5 | 10^3 | 100 |
| 100 | 10^6 | 10^5 | 10 |
| 1000 | 10^7 | 10^7 | 1 |
| 10000 | 10^8 | 10^9 | 0.1 |
| 10^5 | 10^9 | 10^11 | 0.01 |
| 10^6 | 10^10 | 10^13 | 0.001 |
对应不同复杂度的函数,随着输入数据n规模的增大,操作增长数是不同的;
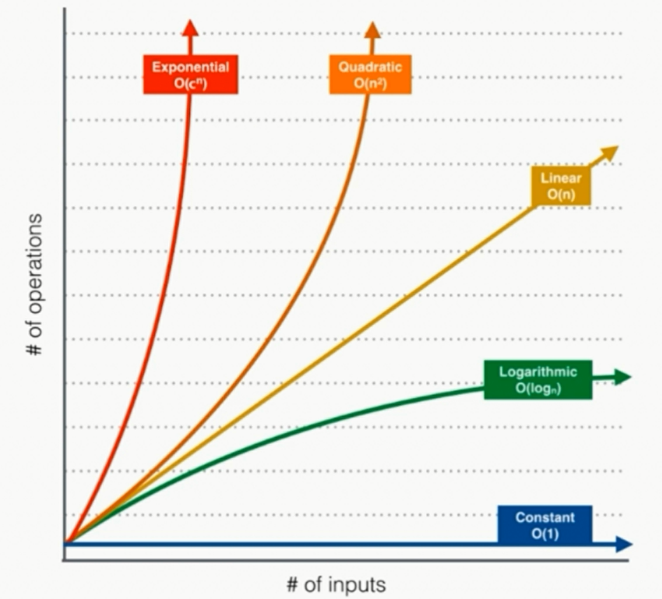
O(1), O(n), O(logn), O(nlogn) 的区别
示例:一个时间复杂度的问题
有一个字符串数组,将数组中的每一个字符串按照字母序排序;之后再将整个字符串数组按照字典序排序。整个操作的时间复杂度?
思路:
- 假设最长的字符串长度为s; 数组中有n个字符串;
- 对每个字符串排序:O(slogs);
- 将数组中的每一个字符串按照字母序排序:O(n*slog(s));
- 将整个字符串数组按照字典序排序:O(s*nlog(n));
结果:
O(n*slog(s)) + O(s*nlog(n)) = O(n*s*logs + s*n*logn) = O(n*s*(logs+logn))
算法复杂度在有些情况和用例相关
| 插入排序算法 O(n^2) | 快速排序算法 O(nlogn) |
|---|---|
| 最差情况:O(n^2) | 最差情况:O(n^2) |
| 最好情况:O(n) | 最好情况:O(nlogn) |
| 平均情况:O(n^2) | 平均情况:O(nlogn) |
对数据规模的概念
如果要想在1s之内解决问题:
- O(n^2)的算法可以处理大约10^4级别数据;
- O(n)的算法可以处理大约10^8级别数据;
- O(nlogn)的算法可以处理大约10^7级别数据;
空间复杂度
- 多开一个辅助数组:O(n)
- 多开一个辅助的二维数组:O(n^2)
- 多开常数空间:O(1)
递归的调用是有空间代价的
示例:
/**
* O(1)时间复杂度 常数级算法
* @param {*} a
* @param {*} b
*/
void swap( int &a, int &b) {
int temp = a;
a = b;
b = temp;
}
/**
* O(n)时间复杂度
* @param {*} n
* @returns
*/
int sum(int n) {
int ret = 0;
for (int i = 0; i <= n; i++)
ret += i;
return ret;
}
/**
* O(n)时间复杂度 1/2*n次swap操作:O(n)
*/
void reverse(string &s) {
int n = s.size();
for (int i = 0; i < n/2; i++)
swap(s[i], s[n - 1 - i]);
}
/**
* O(n^2)
* (n-1)+(n-2)+(nn-3)+...+0
* =(0+n-1)*n/2
* =(1/2)n*(n-1)
* =1/2n^2-1/2*n
* =O(n^2)
*/
void selectionSort(int arr[], int n) {
for (int i = 0; i < n; i++) {
int minIndex = i
for (int j = i + 1; j < n; j++)
if (arr[j] < arr[minIndex])
minIndex = j;
swap(arr[i], arr[minIndex]);
}
}
/**
* O(n^2)?
* 30n次基本操作 O(n)
*/
void printInformation(int n) {
for (int i = 0; i < n; i++) {
for (int j = 1; j <= 30; j++)
cout<<"Class"<<i<<"-"<<"No."<<j<<endl;
return;
}
/**
* O(logn)
* logaN logbN
* logaN = logab * logbN
* (常数)
* O(logn)
*/
/**
* O(logn)
* 二分查找法的时间复杂度是O(logn)的
* 在n个元素中寻找 |
* 在n/2个元素中寻找 |
* 在n/4个元素中寻找 |
* ..... |
* 在1个元素中寻找 ﹀
* n经过几次“除以2”操作后,等于1?
* 对数函数的定义 log2n = O(logn)
*/
int binarySearch(int arr[], int n, int target) {
int l = 0, r = n-1;
while(l <= r) {
int mid = l + (r - l)/2;
if(arr[mid] == target)return mid;
if(arr[mid] > target) r = mid - 1;
else l = mid + 1;
}
return -1;
}
/**
* O(logn)
* 整形转成字符串
* n经过几次“除以10”操作后,等于0?
* log10n = O(logn)
*/
string intToString(int num) {
string s = "";
while(num) {
s += "0" + num%10;
num /= 10;
}
reverse(s);
return s;
}
/**
* O(sqrt(n))
*/
bool isPrime(int n) {
for (int x = 2; x*x <= n; x++)
if( n%x == 0 )
return false;
return true;
}
复杂度试验
如果要想在1s之内解决问题:
- O(n^2)的算法可以处理大约10^4级别的数据;
- O(n)的算法可以处理大约10^8级别的数据;
- O(nlogn)的算法可以处理大约10^7级别的数据;
实验,观察趋势
- 每次将数据规模提高两倍,看时间变化
递归算法的复杂度分析
- 不是有递归的函数就一定是O(nlogn)!(概念:主定理)
- 如果递归函数中,只进行一次递归调用,递归深度为depth;
- 在每个递归函数中,时间复杂度为T;
- 则总体的时间复杂度为O(T*depth);
- 递归中进行多次递归调用
- 计算的调用次数(=递归深度)
- 如果递归函数中,只进行一次递归调用,递归深度为depth;